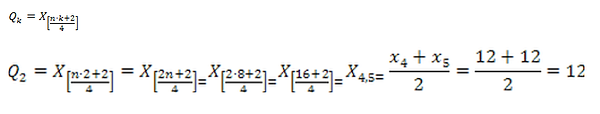ASIMETRÍA Y CURTOSIS
Hasta ahora se han estudiado los parámetros de centralización y de dispersión que son las medidas más frecuentes que se calculan en cualquier estudio estadístico.
Sin embargo existe también medidas que indican de la simetría o asimetría de la distribución y del achatamiento o no de la misma.
Empezando con la simetría, es lógico pensar que si la distribución tiene una única moda y es simétrica, entonces las tres medidas de centralización coinciden. Si no es simétrica, suele suceder que la mediana esté comprendida entre la moda y la media.
Medidas de simetría o asimetría
Miden la mayor o menor simetría de la distribución. Existen dos medidas de este tipo:
* Índice de simetría de Pearson:
Si la distribución es asimetría As sera 0
Si la distribución asimétrica positiva, As sera mayor que 0
Si la distribución es asimetría negativa, As sera menor que 0
* Índice de simetría de Fisher:
EJERCICIO:
Calcular el Coeficiente de Pearson, Medida Cuartílica y la Medida de Fisher dada la siguiente distribución: 6, 9, 9, 12, 12, 12, 15 y 17
Solución:
Calculando la media aritmética se obtiene:
* Para calcular los cuartiles se ordena los datos de menor a mayor
* Calculando el cuartil uno se obtiene:
* Calculando el cuartil dos se obtiene:
* Calculando el cuartil tres se obtiene:
* Calculando la desviación estándar muestral se obtiene:
* Calculando el Coeficiente de Pearson se obtiene:
* Calculando la Medida de Bowley se obtiene
* Calculando la desviación estándar poblacional se obtiene:
* Calculando la Medida de Fisher se obtiene
Datos: Los cálculos en Excel se muestran en la siguiente figura:
Observación: El coeficiente de asimetria (A2:A9) es un valor que tiene consideraciones semejantes a la Medida de Fisher.
EJERCICIO DEL VÍDEO
Esto quiere decir que el coeficiente de asimetria de fisher para una población es hacia la izquierda
Medidas de curtosis
Miden la mayor o menor concentración de datos
alrededor de la media. Se suele medir con el
coeficiente de curtosis:
Si este coeficiente es nulo, la distribución se dice normal (similar a la distribución normal de Gauss) y recibe el nombre de mesocúrtica.
Si el coeficiente es positivo, la distribución se llama leptocúrtica, más puntiaguda que la anterior. Hay una mayor concentración de los datos en torno a la media.
Si el coeficiente es negativo, la distribución se llama platicúrtica y hay una menor concentración de datos en torno a la media. sería más achatada que la primera.
Los resultados pueden ser los siguientes:
g2 = 0 (distribución mesocúrtica).
g2 > 0 (distribución leptocúrtica).
g2 < 0 (distribución platicúrtica).
EJERCICIO DEL VÍDEO