
REGRESIÓN LINEAL MÚLTIPLE
La regresión lineal es una técnica estadística destinada a analizar las causas de por qué pasan las cosas. A partir de los análisis de regresión lineal múltiple podemos:
* Identificar que variables independientes (causas) explican una variable dependiente (resultado).
* Comparar y comprobar modelos causales.
* predecir valores de una variable, es decir, a partir de unas características predecir de forma aproximada un comportamiento o estado.

EJEMPLO:
“Una desea estimar los gastos en alimentación de una familia en base a la información que proporcionan las variables regresoras X1 =“ingresos mensuales” y X2 =“número de miembros de la familia”. Para ello se recoge una muestra aleatoria simple de 15 familias cuyos resultados son los de la tabla adjunta
(El gasto e ingreso está dado en cientos de miles de pesetas)”

RESOLUCIÓN:
Los datos en forma matricial

Con estos datos se obtiene:

Por tanto:

De donde:

El modelo de regresión lineal que se tiene es:
A partir de esta ecuación se obtienen las predicciones y los residuos asociados a las observaciones muestrales. Para la primera observación (X1=2´1; X2=3 y Y=0´43) se obtiene

Razonando así en todos los puntos muestrales se obtiene:

Calculo scR:

También se puede calcular la scR de la siguiente forma:
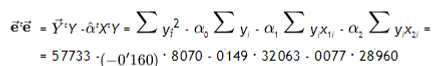
Se calculan los intervalos de confianza de los parámetros del modelo al 90%,:


Con estos datos se obtiene el siguiente contraste conjunto de la F:

El contraste conjunto de la F indica claramente la influencia del modelo en la variable respuesta. Por tanto, de los contrastes individuales y del conjunto se deduce la influencia de cada una de las dos variables regresoras y la influencia conjunta del modelo.
Ahora se calcula el contraste individual de la F respecto a la variable x2=“tamaño”, contraste que es equivalente al contraste individual de la t. Para ello, se obtiene la regresión de la variable gasto respecto a la variable ingreso,
Gasto = 87´124 + 1´543 ingreso
la tabla ANOVA de este modelo es:

La variabilidad incremental debida a la variable diámetro es:
este valor indica lo que aumenta la variabilidad explicada por el modelo al introducir la variable tamaño.
Para contrastar la influencia o no de esta variable se utiliza el estadístico:

que da el mismo p-valor que en el contraste individual de la t (hay pequeñas diferencias por los resondeos).
Cálculo de los coeficientes de correlación:

La tabla ANOVA del modelo es:

Análogamente, el coeficiente de correlación simple entre las variables gasto y tamaño es,

Coeficiente de correlación parcial entre las variables gasto e ingreso.:

Otra forma más compleja de calcular este coeficiente es la siguiente: se obtienen las siguientes regresiones y se guardan los residuos,

Ahora el coeficiente de correlación parcial entre las variables gasto e ingreso se obtiene como el coeficiente de correlación simple entre las variables Egasto.tamaño y Eingreso.tamaño

este coeficiente mide la relación entre las variables gasto e ingreso libres de la influencia de la variable tamaño.
Análogamente se obtiene que
Estimación de la media condicionada.


Algunos gráficos de interés que ayudan a resolver el problema son los siguientes:
Gráficos parciales de las componentes


Gráficos de residuos:




